FHNO: Kinetics

Fourier-Hermite Neural Operator for Rarefied Gas

PyTorch Neural Operators Boltzmann Eq
Model Predictions

Predicting Gas Transport in Porous Media

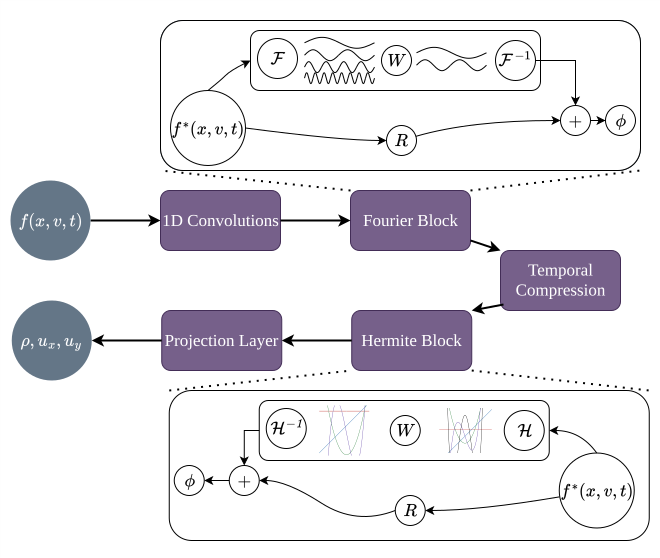
Transient to
Steady State

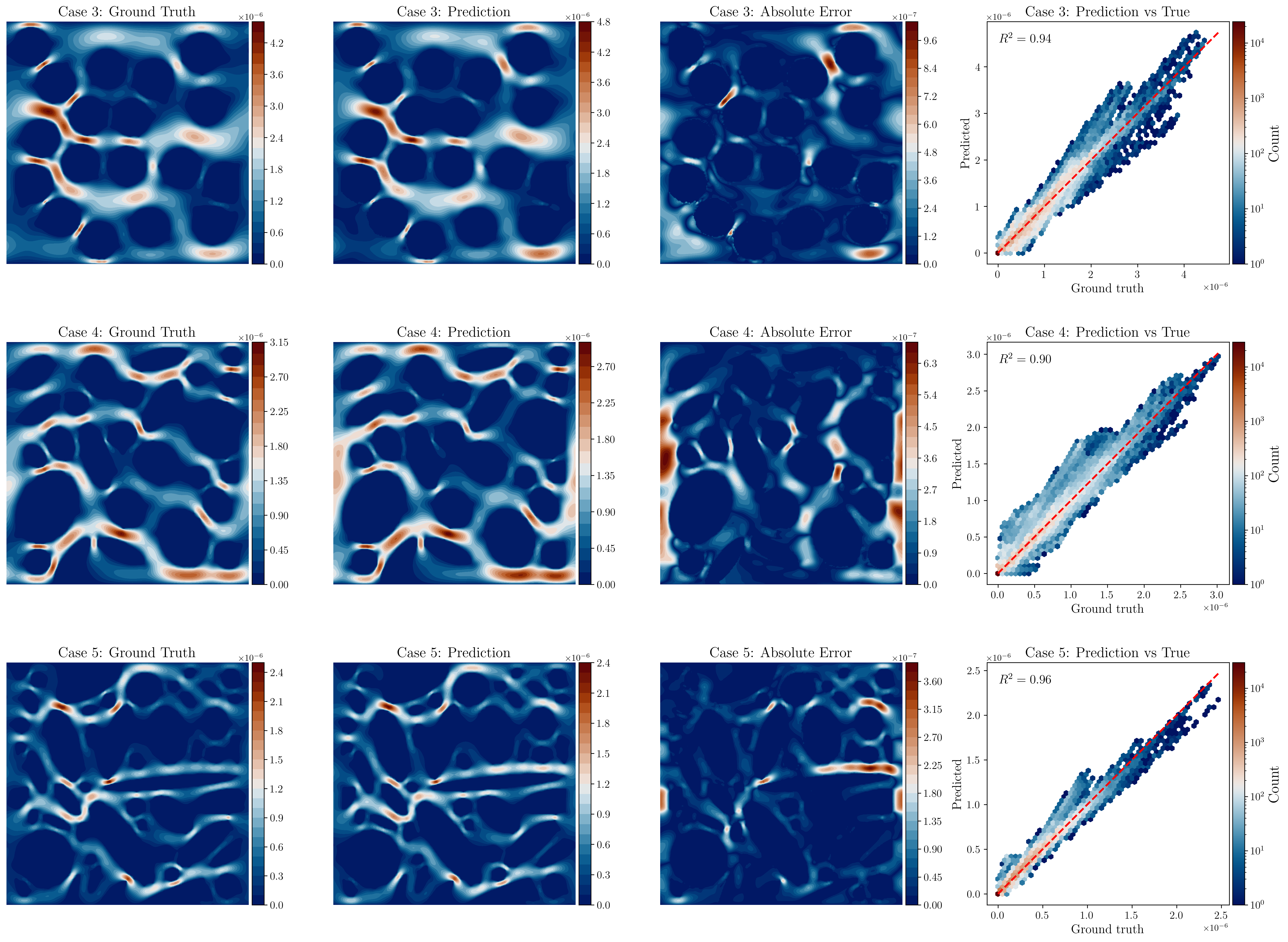
The Fourier-Hermite Neural Operator (FHNO) is a novel architecture designed to map the initial $N$ transient iterations of a simulation to its corresponding steady-state solution.

By combining Fourier spectral blocks with Hermite chaos expansions, FHNO captures rarefied gas dynamics in complex porous media, significantly performing standard FNO and HNO approaches.

Model Performance

  • Optimal Input Depth: $N=600$
  • Accuracy ($R^2$): ≥ 0.90
  • Super-resolution: 4x Upscaling
01. Methodology

Deep Learning Architecture

The network input is a tensor $\mathbf{f}\in\mathbb{R}^{C\times T}$, where each entry $f_i(t)$ represents the distribution function corresponding to discrete direction $i$ (for D2Q9 lattice) at time $t$. The architecture proceeds in three key stages:

1. Temporal Lifting

We apply 1D convolutions along the temporal axis to lift the input distributions into a high-dimensional feature space.

$$ x^{(\ell)}_c(t) = \phi \left(\sum_{m=1}^{C_{\ell-1}} \sum_{\tau=0}^{K-1} k^{(\ell)}_{c m}(\tau)\, x^{(\ell-1)}_m(t-\tau) + b^{(\ell)}_c\right) $$
FHNO Architecture

2. Fourier Spectral Blocks

Long-range temporal correlations are modeled by mixing channels in the frequency domain. We retain only the lowest $K$ frequency modes.

$$ \tilde{Y}_c(k) = \sum_{m=1}^{C} \tilde{X}_m(k) \big( W_{m\to c,\mathrm{r}}(k) + i\, W_{m\to c,\mathrm{i}}(k)\big) $$

Hermite Chaos & Reconstruction

The final stage operates in the localized kinetic moment space. We project the channel features back onto the D2Q9 lattice basis using Hermite polynomials up to the second order.

$$ \hat{f}_i = w_i \bigg( \tilde{a}_0 + \sum_{\alpha} H_1^{\alpha}(i)\,\tilde{a}_1^{\alpha} + \frac{1}{2}\sum_{\alpha,\beta} H_2^{\alpha\beta}(i)\,\tilde{a}_2^{\alpha\beta} \bigg) + \gamma_i\, s_i $$

Output: Steady-State Distribution $\Rightarrow$ Macroscopic Velocity

← Back to Projects